0.0017×100: Small numerical values, such as 0.0017, may appear trivial at first, but they play a crucial role in a variety of sectors, including finance, scientific research, and business operations. When you multiply 0.0017×100, you get 0.17. This transformation, although it might seem straightforward, can have meaningful implications in practical contexts.
In finance, for example, precise decimal values are essential for accurate calculations of interest rates, investments, and financial forecasts. A small percentage change, like 0.17%, can influence investment returns or financial reports significantly over time. In scientific research, such exact figures are used to measure and report minute quantities, such as concentrations of substances in experiments or small changes in data readings, which are critical for valid results and conclusions.
In business, especially in sectors like inventory management or pricing strategies, small numbers can affect profit margins and cost calculations. Understanding how to work with these figures accurately can help in making informed decisions and optimizing operations.
By delving into how multiplying 0.0017×100 results in 0.17, this article sheds light on how such mathematical operations are more than just numbers; they represent significant shifts that can impact various facets of our daily lives. Recognizing the value of these small figures and their practical applications underscores the importance of precision and attention to detail in both professional and personal contexts.
Grasping the Significance of 0.0017×100
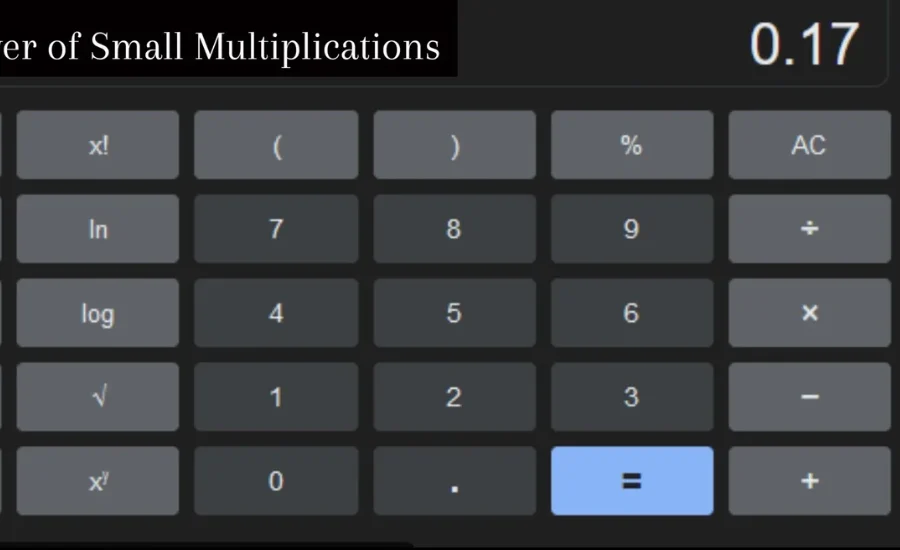
UUnderstanding how to multiply decimal numbers is a fundamental skill that can be easily mastered with a few clear steps. Consider the multiplication of 0.0017×100, which yields a result of 0.17. This example illustrates how a straightforward calculation can be applied in various practical contexts.
Here’s a detailed breakdown of the process:
- Identify Decimal Places: Begin by noting the number of decimal places in the initial number. For 0.0017, there are four digits to the right of the decimal point. Recognizing this is crucial for correctly performing the multiplication.
- Shift the Decimal Point: When you multiply a decimal number by 100, you effectively move the decimal point two places to the right. This is because multiplying by 100 is equivalent to scaling the number up by a factor of 100, which involves a positional shift in the decimal system. In this case, moving the decimal point two places to the right transforms 0.0017×100.
- Perform the Multiplication: After shifting the decimal point, the result of multiplying 0.0017×100. This process highlights how decimal multiplication affects the value, making it essential to understand the positional value of the decimal point.
This method of decimal multiplication is widely applicable across different fields. In finance, accurate decimal calculations are crucial for determining interest rates, investment returns, and financial forecasts. In scientific research, precise decimal values are necessary for measurements and data analysis, where even small changes can significantly impact results. In business, understanding how to handle decimal values efficiently can aid in inventory management, pricing strategies, and cost calculations.
Mastering these basic principles of decimal multiplication allows for more accurate and effective problem-solving in both professional and everyday scenarios. By applying these steps, you can handle various calculations with confidence and clarity.
Applications of Multiplying 0.0017×100
Finance: Precision in Financial Calculations
In the financial world, even small numbers like 0.0017 play a significant role. For instance, when multiplied by 100, 0.0017 becomes 0.17. This conversion can make financial figures more relatable and easier to understand.
Interest Rates: Banks often use decimal figures for interest rates on savings accounts. When you multiply a rate of 0.0017×100, it translates to 0.17%. This percentage is more intuitive for customers and helps them better grasp the interest earned.
Profit Margins: Businesses may encounter low profit margins such as 0.0017. Converting this to 0.17% by multiplying by 100 provides a clearer perspective on the profitability of a product or service, making it easier to communicate to stakeholders.
Science: Enhancing Precision in Research
In scientific research, dealing with very small quantities is common. Multiplying 0.0017×100 helps translate these tiny figures into more practical values.
Chemical Solutions: For example, a chemical solution with a concentration of 0.0017 Molar (M) can be converted to 0.0017×100. This makes the solution’s concentration more manageable for experimental procedures.
Physics Measurements: In physics, small measurements such as 0.0017 can be scaled up to 0.17 for practical use in experiments, making it easier to work with and interpret data.
Data Analysis: Simplifying Numeric Data
Data analysts often work with small figures, and multiplying numbers like 0.0017×100 can simplify the analysis process.
Data Normalization: For large datasets, analysts may scale small numbers up by multiplying them by 100 to facilitate comparison and analysis. This practice helps in making data more comparable and interpretable.
Machine Learning: In machine learning, scaling small numerical values like 0.0017×100 is a common technique. This adjustment can enhance the performance of algorithms and models, ensuring they operate effectively with the given data.
By understanding and applying these conversions, professionals across finance, science, and data analysis can enhance their precision and clarity in various tasks.
Healthcare: Enhancing Precision in Laboratory Tests

In medical laboratories, precision in measurements is crucial for obtaining accurate results and ensuring effective treatments. For example, when preparing solutions for diagnostic assays, a concentration of 0.0017 grams per liter is often used. This figure, while small, needs to be accurately handled to ensure the reliability of test results. By multiplying 0.0017×100 the concentration is scaled to 0.17 grams per liter. This adjustment simplifies the measurement process, making it easier for laboratory technicians to prepare solutions with greater precision. Accurate dosages and solution concentrations are essential for conducting reliable tests and achieving valid diagnostic outcomes.
Environmental Science: Scaling for Policy and Regulation
Environmental scientists often measure pollutant concentrations at very low levels, such as 0.0017 parts per million (ppm). This small value can be challenging to communicate effectively, both to policymakers and the public. To make this information more accessible, multiplying 0.0017×100 converts it to 0.17 ppm. This scaling enhances clarity, allowing for easier interpretation of pollution levels and more effective communication of environmental data. Such adjustments are vital for formulating and implementing environmental regulations and policies, as they help convey the significance of pollution levels in a manner that is both comprehensible and actionable.
Engineering: Quality Control in Manufacturing

In the engineering and manufacturing sectors, precision in measurements is key to ensuring that components and assemblies meet stringent quality standards. For instance, a tolerance level of 0.0017 millimeters might be specified for a critical component. To facilitate inspection and quality control, this measurement can be scaled up by multiplying 0.0017×100, resulting in 0.17 millimeters. This conversion makes it easier for engineers and quality control personnel to assess whether components meet required specifications and to ensure that parts fit together correctly. Such precision is crucial for maintaining the functionality and safety of engineered products.
Finance: Evaluating Microtransactions
In the financial industry, especially within the realm of digital transactions and microtransactions, even small amounts need precise handling. For example, a transaction amount of 0.0017 units of currency may be involved in micro-payments or fractional transactions. To simplify accounting and reporting, multiplying 0.0017×100 results in 0.17 units of currency. This adjustment helps streamline financial processes by making the values more manageable and easier to understand. Accurate handling of such small amounts is essential for ensuring the integrity of financial transactions and effective management of digital accounts.
Data Science: Enhancing Statistical Models
Data scientists frequently work with small numerical values in statistical models and predictive analytics. A probability value as small as 0.0017 might be used in risk assessments or data simulations. To improve the usability of these values in statistical calculations, multiplying 0.0017×100 converts it to 0.17. This scaling makes it easier to integrate these values into models and interpret the results effectively. Accurate scaling of small values enhances the performance of data models and ensures more reliable predictions and analyses.
Education: Simplifying Mathematical Concepts

In educational settings, particularly in mathematics instruction, students often struggle with understanding small decimal values. For instance, demonstrating how to multiply 0.0017×100 to obtain 0.17 provides a practical example of decimal place shifting. This approach helps students grasp the concept of scaling numbers and understanding their practical applications. By illustrating these calculations in a clear and relatable manner, educators can improve students’ comprehension of decimal operations and their relevance in real-world scenarios.
The process of multiplying 0.0017×100 plays a significant role across various fields, from healthcare and environmental science to engineering, finance, data science, and education. This simple mathematical operation transforms small, challenging values into more manageable figures, enhancing precision, communication, and practical application in each respective domain.
Also read: 10027.5 716.25
Final Words
The multiplication of 0.0017×100, resulting in 0.17, might seem like a simple mathematical operation, but it plays a critical role across a variety of fields. In finance, this conversion can make small interest rates more comprehensible, turning a seemingly insignificant 0.0017% into a more relatable 0.17%. This small adjustment can have significant implications for understanding investment returns, profit margins, or financial forecasts.
In scientific research, where precision is paramount, multiplying 0.0017×100 can help transform minute concentrations into more manageable figures, essential for accurate experiments and data analysis. For data analysts, scaling small values by this factor simplifies comparisons and enhances the performance of models, making the data more accessible and easier to interpret.
In healthcare, particularly in laboratory settings, this operation ensures precision in measurements, which is vital for accurate diagnostics and treatments. Similarly, in environmental science, converting 0.0017 parts per million to 0.17 parts per million makes it easier to communicate critical data on pollutant levels, aiding in the formulation of effective regulations and policies.
Whether in finance, science, education, or engineering, understanding and applying the multiplication of 0.0017×100 demonstrates how even small numerical values can have a significant impact. This simple yet powerful operation enables better decision-making, clearer communication, and more effective problem-solving across various professional and personal contexts.
FAQs
1. What does 0.0017×100 equal?
When you multiply 0.0017 by 100, the result is 0.17. This simple calculation can have practical implications in various fields, such as finance, science, and data analysis.
2. Why is multiplying 0.0017×100 important?
Multiplying 0.0017×100 is important because it transforms small, precise values into more manageable numbers, making them easier to interpret and apply in real-world scenarios like financial calculations, scientific experiments, and data analysis.
3. How is 0.0017×100 used in finance?
In finance, multiplying 0.0017 by 100 can convert small interest rates or profit margins into percentages that are easier to understand, facilitating better decision-making and financial planning.
4. What role does 0.0017×100 play in scientific research?
In scientific research, multiplying 0.0017×100 can help scale small measurements, such as concentrations in chemical solutions, to more practical values, ensuring accurate experiments and data interpretation.
5. How does 0.0017×100 affect data analysis?
In data analysis, multiplying small values like 0.0017 by 100 can simplify the process of comparing and analyzing large datasets, making the data more accessible and easier to work with.
6. Can 0.0017×100 be applied in healthcare?
Yes, in healthcare, particularly in laboratory settings, multiplying 0.0017 by 100 ensures precision in measurements, which is crucial for accurate diagnostics and treatment planning.
7. How is 0.0017×100 relevant to environmental science?
In environmental science, converting 0.0017 parts per million to 0.17 parts per million through multiplication by 100 makes pollution data more comprehensible, aiding in the communication and implementation of environmental policies.
8. What is the significance of 0.0017×100 in education?
In education, teaching students to multiply 0.0017 by 100 helps them understand decimal operations and their real-world applications, improving their mathematical comprehension and problem-solving skills.
9. How does 0.0017×100 impact engineering and manufacturing?
In engineering and manufacturing, multiplying small measurements like 0.0017 by 100 helps ensure precision in quality control and inspection, maintaining the accuracy and functionality of components and assemblies.
10. What are the broader implications of understanding 0.0017×100?
Understanding how to multiply 0.0017 by 100 allows professionals across various fields to make informed decisions, communicate more clearly, and solve problems more effectively by handling small numerical values with precision.
For a deeper dive into related topics and more, visit Discover thrill.









Leave a Reply
View Comments